有了良好的資料前處理和特徵工程，仍舊不能讓機械產生學習。能夠讓機械產生學習，仰賴的是一個最佳化的演算法。

LinearClassifier 預設最佳化演算法是 Ftrl Optimizer。 在這裡為了能與往後的主題連貫，將會使用較為簡單的梯度下降學習法（gradient descent）。梯度下降學習法的中心思想，是利用疊代的方式來更新參數。疊代方法中，先從一個隨機的初始值開始，再經由多次疊代更新訓練資料所提供關於 loss function 的資訊（如梯度）後，達到最佳化的結果。每次疊代中，都會將舊的參數加上當次疊代所計算出來的梯度，來作為下一疊代的參數的更新值。一次疊代，被稱為 epoch，而每一個 epoch 結束時，都需要見過所有的訓練例子。此外，演算法還需要用一個名為 learning rate 的參數來控制每一次疊代中更新的步距。若 learning rate 設為 1，則使用在該次疊代算出的梯度為步距。但通常，learning rate 會設定成遠小於 1 的數目。

圖一：本圖是根據 Machine Learning Crash Course 改編所繪成。如同在 Crash Ｃourse 所示，一個最簡單 loss function，可以是一個開口向上的拋物線圖形（左上），這樣的 loss function 屬於 convex function 的一種，可保證只有一個全域的最低點。可以看到圖一左下，能夠到達最低點的方向，恰巧是與梯度相反的方向，所以在每次疊代更新時，都取和梯度相反的方向來做更新。

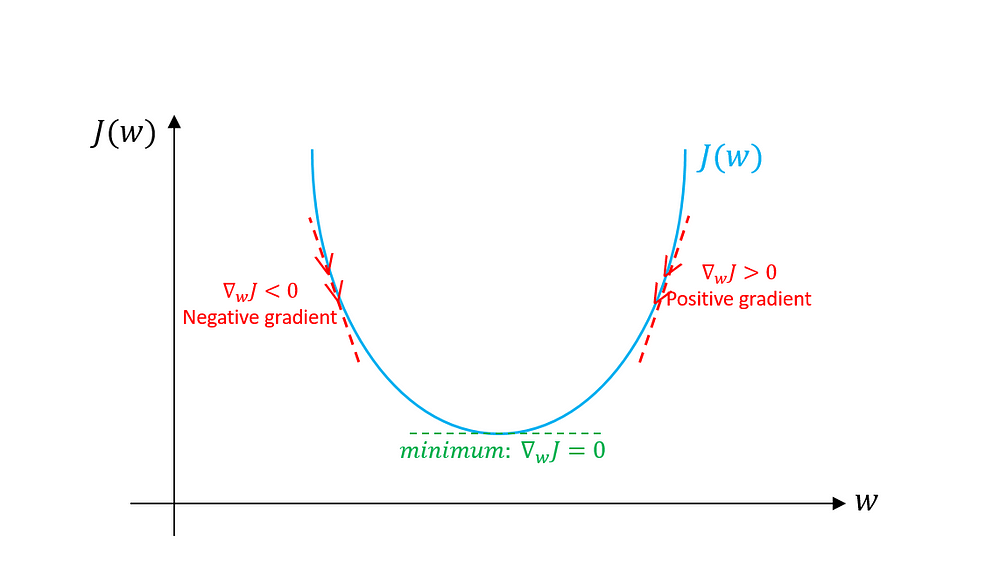
圖二：說明如何計算梯度的方向

梯度演算法步驟：

1. 初始化參數為任意值（圖一右上）
2. 在 i 次疊代，計算出下一次疊代（i+1）的參數值，根據此公式：W(i+1) = W(i) - g(i) * lr （圖一右下）
   • g(i) 為在該點計算出的梯度，可由泰勒展開式一階逼近求得，恰巧是通過 W(i) 的切線斜率。
   • lr 是 learning rate
3. 當 loss function 到達最低點或超過最大疊代數時，停止疊代

梯度下降演算法有許多不同的變形，可大致分為以下幾種：

1. 對餵送資料所做的變化處理
2. 對設定 learning rate 所做的變化處理

對餵送資料所做的變化處理

為了針對避免過度學習或在文獻上多稱為的過度擬合（overfitting）梯度下降演算法可使用一種叫做 mini-batch 的方式餵送資料。與其每次疊代都使用全部的訓練資料，mini-batch 的方式，將全部的資料分為幾個不同的批次，分批遞送。這樣做的好處，在於計算梯度時，可以探索不同的方向，在較為複雜的 loss funciton surface，可以找到更加的最佳值。

圖三就是梯度下降演算法使用所有的資料（full batch or batch gradient descent），和使用 mini-batch gradient descent 的分別。在圖三中所指的 Stochastic Gradient Descent 是指每個批次只使用一個訓練例子來計算梯度。但在許多的文獻中，Stochastic Gradient Descent 通常也包含 mini-batch gradient descent。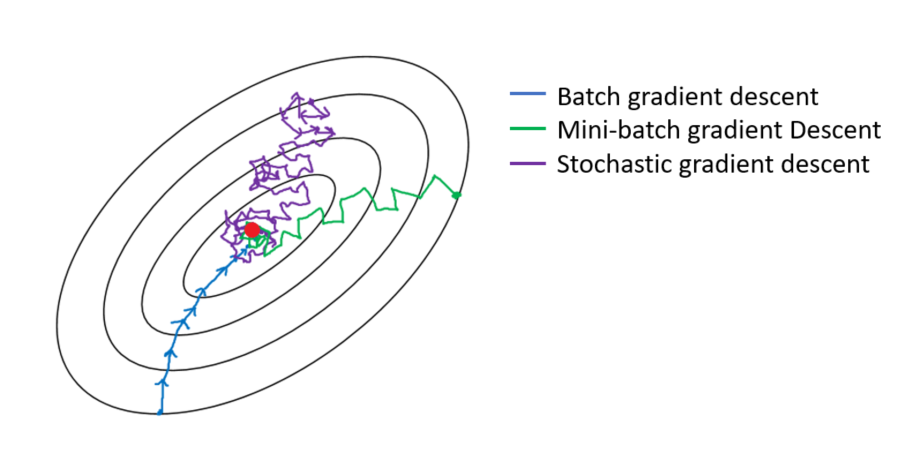

而在 Tensorflow 中使用梯度下降學習法，以及使用 full-batch 和 mini-batch 的程式碼例子如下：

#full-batch
data_frame = pd.read_csv(filepath)
features = dict(data_frame)
labels = feature.pop('Survived')
full_batch_ds = tf.data.Dataset.from_tensors((features, labels))

# mini-batch batch-size = 10
mini_batch_ds = tf.data.Dataset.from_tensor_slices((features, labels)).batch(10)

# mini-batch (completely stochastic) batch-size = 1
single_batch_ds = tf.data.Dataset.from_tensor_slices((features, labels)).batch(1)

對設定 learning rate 所做的變化處理

簡單的梯度下降學習法中，learning rate 是在整個訓練過程保持固定的。然而，這樣的設定並不適合較為複雜的 loss function surface，所以就有人利用了 Momentum 的觀念，針對 loss function surface 的局部狀況，動態調整 learning rate。

對於 Momentum 最直觀的解釋，是將演算法當成在 loss function surface 行進的球，若是在陡峭的坡度上前進，則靠著過去動量提供的速度前進。若是在較為平緩的表面上前進，則減緩速度以錯過可能的最佳值。坡度可以當作演算法對 loss function 所計算的梯度，根據動量變化而得到的加速度，則可以看作對 learning rate 的調整。若以數學式表示，在更新參數時，則是將過去的參數更新值考慮在內，並與現在的梯度更新做線性組合，形成這次疊代的更新值。

另外一種方法，則是動態改變 learning rate（adaptive learning rate）。動態改變 learning rate 是為了解決不同的參數需要不同 learning rate 的問題，通常這個問題來自於參數的維度過高，而資料在參數空間裡呈 sparse 分佈的問題，以至於有些參數更新的頻率並沒有很高。欲對不同參數產生不同的 learning rate，是對過去 gradient 計算 l2 norm 或 weighted 的平均值，再由這些值來決定每個參數 learning rate 的變更。

Momentum 和 adaptive learning rate 方法都可以使用 mini-batch 的方式來學習。

在 Tensorflow 可中使用 AdaGrad 最佳化演算法（tf.train.AdagradOptimizer）來達到動態改變 learning rate，而 Momentum 方法，則需使用（tf.train.MomentumOptimizer）

在了解了梯度下降演算法後，必須談到一個很重要的觀念，可以大幅的幫助梯度下降學習的速度。那就是，梯度下降演算法，受到 loss function surface 的形狀所影響。梯度下降演算法較偏好圓形的 loss function surface，因為如此一來，無論將參數初始化在 surface 中任何一個點都能耗費相同時間抵達最低點。若 surface 是成橢圓形，則初始化在較長的一軸時，就必須耗費較長的時間達到最低點。

能夠改善這種情況，通常會隊訓練資料做標準化的前置處理，在這個標準化的前置處理中，需要減去這個批次內資料的 mean 和 除上 standard deviation， 將資料的數值形成一個像 Gaussian 其 mean 為零， standard deviation 為 1 的分佈。

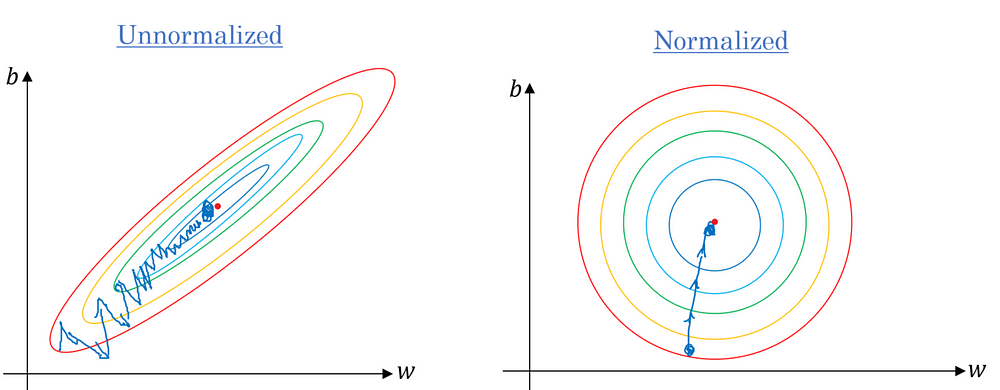
圖四左圖是未經過標準化的 loss function surface，可以看到若初始化在長軸的一端，需要耗費更長的時間才能到達最低點。右圖則是經過標準化 loss function surface，可以看到此 surface 形狀較少受到初始值的影響。

以下的程式碼，則是對數值特徵 Fare 和 Age 做標準化。

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
scaler.fit(train_data[['Fare', 'Age']])

fare = tf.feature_column.numeric_column('Fare', normalizer_fn=lambda x: ((x - scaler.mean_[0])/scaler.scale_[0]))
age = tf.feature_column.numeric_column('Age', normalizer_fn=lambda x: ((x - scaler.mean_[1])/scaler.scale_[1]))

在前面的程式碼中，我們利用 scikit-learn 的 MaxMinScaler 來做正規化，而將數值壓縮在 0 和 1之間也是相同的道理，只不過這樣的做法並不能保證資料數值會形成一個像圓形的分佈，而只是
線性的對原數值做同比例壓縮。 這個方法雖然不像標準化有理論基礎，但是同樣也能確保所有的特徵值都能擁有相同的數值距離。因為，若有一個特徵，其數值距離與其他的特徵值相差太大，也會造成以上所說的問題。

在下篇中，我們將要解說如何避免過度學習的方法。

圖片來源:

圖一：Machine Learning Crash Course：Gradient Descent
圖二，三，四來自：Toward Data Science: Gradient Descent Algorithm and Its Variants